Contents
競争して勝つ先にあるもの
医師として誰よりも頑張る。他の医師が持たない知識や経験、高い技術を身につける。
そうすれば、将来努力に比例した高額の報酬、安定したポジションを得ることができるのでしょうか?
今回は競争して勝つ先にあるものについて考えてみましょう。
競争するとみんなと同じ方向に向かってしまうというジレンマ
医師は、受験勉強を勝ち抜いた社会的エリートとされる人が多く集まる職業です。
試験で良い点を取れば医学部に合格する。社会人になってからも、人より高得点をとって、競争に勝つためには何をすべきか?と考えてしまう医師が多いかもしれません。
しかし、一つはっきりとしていることは、「医師として激しい競争に参加すると、みんなと同じ方向に向かってしまうジレンマ」があります。
激しい競争のイメージとしては、大学病院などのアカデミックポジションでライバルとしのぎを削る戦いをして、その競争に勝ち抜いて教授になるというキャリアがイメージしやすいですね。
アカデミックポジションにおける勤務医の年収に関しては、おそらく正規分布になるはずです。
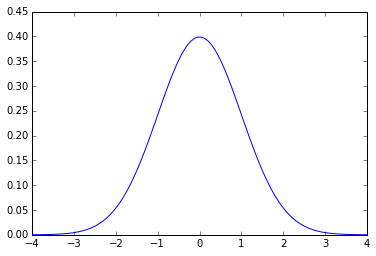
例えば、アカデミックポジションにおける成功者の代表として教授の年収について考えてみましょう。
年収2000万円の教授もいれば、1500万円の教授もいるでしょう。もしかしたら、3000万円稼ぐ教授もいるかもしれません。でも、1億円稼ぐ教授や年収が200万円の教授は日本にはいないかもしれません。
これは、努力すればするほど年収が上がるわけではなく、一般的に期待される年収が正規分布に従っているためです。
リアルビジネスにおける成功はべき分布
橘玲さんの書籍の中で、ベル・カーブ(正規分布)とロングテール(べき分布)の違いについて述べられています。
マンデルブロは確率的世界の外側に広大な「複雑系世界」があると考えた。確率的世界はベルカーブ(正規分布)で予測できるが、複雑系世界はロングテール(べき分布)なので、正規分布で表すことはできない。
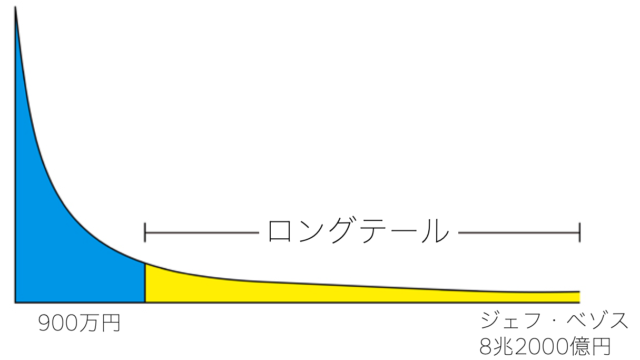
ロングテール(べき分布)については、アメリカ人の世帯年収を例にとって考えてみましょう
アメリカ人世帯の平均的な資産のボリュームゾーンは900万円前後だそうです。
それに対して、Amazonのジェフ・ベゾスの資産は8兆2000億円です。
ベル・カーブ(正規分布)については、身長を例にとって考えてみましょう。
日本人男性の平均身長は170cm前後とされています。
2mを超える人は、非常に稀であり、長い人類の歴史を考えてみても、身長が5mを超える日本人はいません。
先程の、アメリカ人世帯の資産のボリュームゾーンである900万円を日本人の平均身長(170cm)に置き換えてみると、ジェフ・ベゾスの身長は227kmです。
世界中の人々が行き交うアメリカの空港で、170cmの日本人のとなりを身長227kmのジェフ・ベゾスが歩いている世界。これが複雑系と呼ばれる世界(私達の生活する資本主義経済も複雑系です)です。
これは、正規分布では起こりえない現象ですが、べき分布のロングテール(恐竜のしっぽ)においては、「非常に珍しいけれども、時におこる現象」と言われています。
経済危機のブラックスワンもロングテールのイベントと認識されるようになりました。
複雑系の世界で起こる重大なイベントはロングテールの世界
先程の例でいえば、競争の先に待つ成功。教授の年収については正規分布として説明ができました。
でも、私達が生活する資本主義経済においては、重大なインベントはべき分布(ロングテール)で起こっています。
アメリカの空港でたまたますれ違った人物(ジェフ・ベゾス)の身長が227kmということが起こり得る世界においては、激しい競争の世界の辺境にはとんでもない成功が意外と多く眠っていることが理解できます。
もっとも、その成功を掴むことは、たやすいことではないでしょうが、激しい競争の世界から一歩距離をおいて、そこで広がる広大な世界で自分の求める成功を探してみることは、意外と期待値が高いことなのかもしれません。











コメント